問題は阪大のホームページから確認してください。2024年12月22日現在はまだ載っていませんが…
(1)
(1) ![]()
(2)
回転軸であるため
(2) 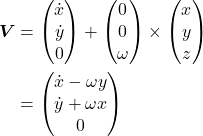
と(1)より、Lagrangian は、
(3) ![]()
(3)
(2)より、
(4)
質量中心(重心)は原点より、
(4) ![]()
相対距離は、符号に気をつけて、
(5) ![]()
これらを連立することにより、
(6) 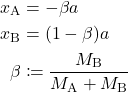
(5)
力の釣り合いより、
(7) 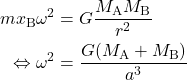
(6)
Lagrange point
(8) ![]()
(7)
(6) の両辺を
(9) 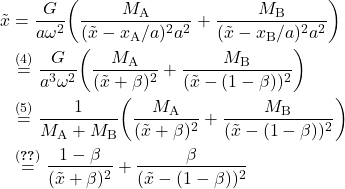
(8)
(10) ![]()
を(7)に代入すると、
(11) 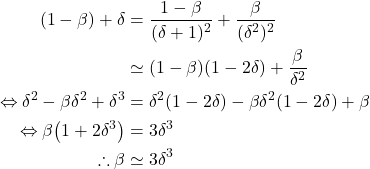
(9)
(8)より、求める距離
(12) ![]()
ここで、
(13) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \delta &\simeq \sqrt[3]{\frac{\beta}{3}}\\ &= \sqrt[3]{\frac{M_{\text{B}}}{3(M_{\text{A}} + M_{\text{B}})}}\\ &= \sqrt[3]{\frac{1}{3} \frac{5.97 \times 10^{24}}{5.97 \times 10^{24} + 1.99 \times 10^{30}}}\\ &\simeq \sqrt[3]{\frac{1}{3} \frac{6.0\times 10^{24}}{2.0 \times 10^{30}}}\\ &=0.01. \end{split}\end{equation*}](https://phlogy.com/wp-content/ql-cache/quicklatex.com-9e76cb09159cc13f917634ad93369741_l3.png)
よって、
(14) ![]()


コメント